In this post, I'll talk about the limitations associated with the conventional binary counter design in terms of it's maximum operating frequency, and also discuss an ingenious yet simple design (not invented by me!) which can operate at a very high frequency.
Conventional Binary Counter: The operating speed of any binary counter, or for that matter, any sequential circuit is governed by the setup time limitation that the combinatorial logic between any two registers (flip-flops). Note that:
- Any higher-order counter bit toggles only when all the lower-order bits are logic 1.
- The input for any higher-order counter bit is a function of all the lower-order bits and itself during the last clock cycle.
- The operating speed for an n-bit counter is limited by the following equation:
Time Period of the Clock ≥ T(clk-to-q),FF0 + (n-2).TAND + TXOR + Tsu,FF(n-1)
- The following figure shows the circuit for a 4-bit conventional binary counter. It must be noted as as the counter width increases, the operating frequency decreases.
High Speed Binary Counter: How about designing a binary counter where there is no combinatorial cells between any two registers, so that such a design is able to achieve the highest operating frequency for a given technology node? For this counter the basic premise is:
- Since the counting sequence for any counter bit is deterministic in nature, it should be possible to design a counter in a manner that: each bit is a function of only itself over all the previous clock cycles.
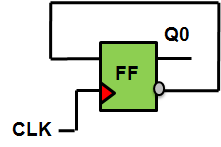
- Johnson Counter enables us to design in such a manner that there is
no combinatorial cell between any two registers. Let's have a look:
Since the LSB i.e. Q0 toggles itself at every clock cycle, the 1-bit Johnson Counter can be used for Q0. Note that here we are using bit-by-bit synthesis instead of the conventional Karnaugh map approach to design our binary counter.
- Similarly, higher order counter bits can be realized by higher order Johnson Counter, where the last bit would represent the binary counter bit. For Q1, the circuit would be:
- The same can be extended in a recursive manner to design any n-bit binary counter.
- Note that in this design, there is absolutely no combinatorial cells between any two registers, thereby making high operating speed possible.Time Period of the Clock ≥ T(clk-to-qbar),FF + Tsu,FFWhat is the trade-off here? The answer is dynamic power dissipation. Note that a conventional n-bit counter would use n flops. However, for the proposed design, 3-bit counter would need (1+2+4=) 7 flops, 4 bit counter would need (1+2+4+8=) 15 flops and so on. This design might find practical application for lower order counter widths like 4-6.Above that, the design would dissipate too much power to be of any practical use.



Very good post. Thanks. I have already familiar with Johnson counter but I havent known the usage.
ReplyDeleteThanks! Even I hadn't realized this part before I came across a paper.
ReplyDeleteI have a problem for you. Could you also design a Gray Counter using a Johnson Counter?
I'd be looking forward to your response! :)
Yes, its cheaper. Johson counter is also a gray counter :)
ReplyDeleteIndeed, it is! :) In fact, I published a defensive publication on the same. http://ip.com/IPCOM/000232249
DeleteCongrats but I could not reach this design. Is ip.com simular to opencores? however it is not free.
DeleteHey Hasan! Thanks! :)
DeleteNo worries. Drop me your e-mail ID, and I'll mail it to you. :)
Hi Naman,
ReplyDeleteCorrect me if I am wrong,
an n-bit Johnson counter can counts till 2n(Ex 3-bit Counter: 000,001,011,111,110,100,000[repeats]).
For 3-bit binary counter(8 states) a 4-bit johnson counter(4 Flops) can be sufficient why we need 7 flops.
For 4-bit binary counter(16 states) an 8-bit johnson counter(8 Flops) can be sufficient why we need 15 flops.
Hi, Naman,
ReplyDeleteHave one question to consult: with what software how do u make these beautiful circuit diagrams?
Sincerely,
Eric